Área bajo la curva mediante la integración por partes

Calcular el área de la región limitada por la gráfica de la función \(y=e^{-x} \ \  sen(x), \ \ el \ \  eje \ \ {x} \ \ en \ \  el \ \ intervalo \ \ [ 0,\pi ]\).

Solución

Graficamos la función realizando una tabulación, es decir, dándoles valores a \( x \ \  de \ \  0 \ \ a \ \ \pi\) para que nos de los respectivos rangos o imágenes correspondientes a dicho dominio.

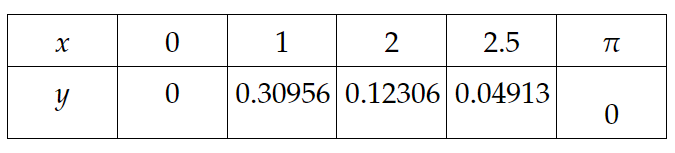
Grafica

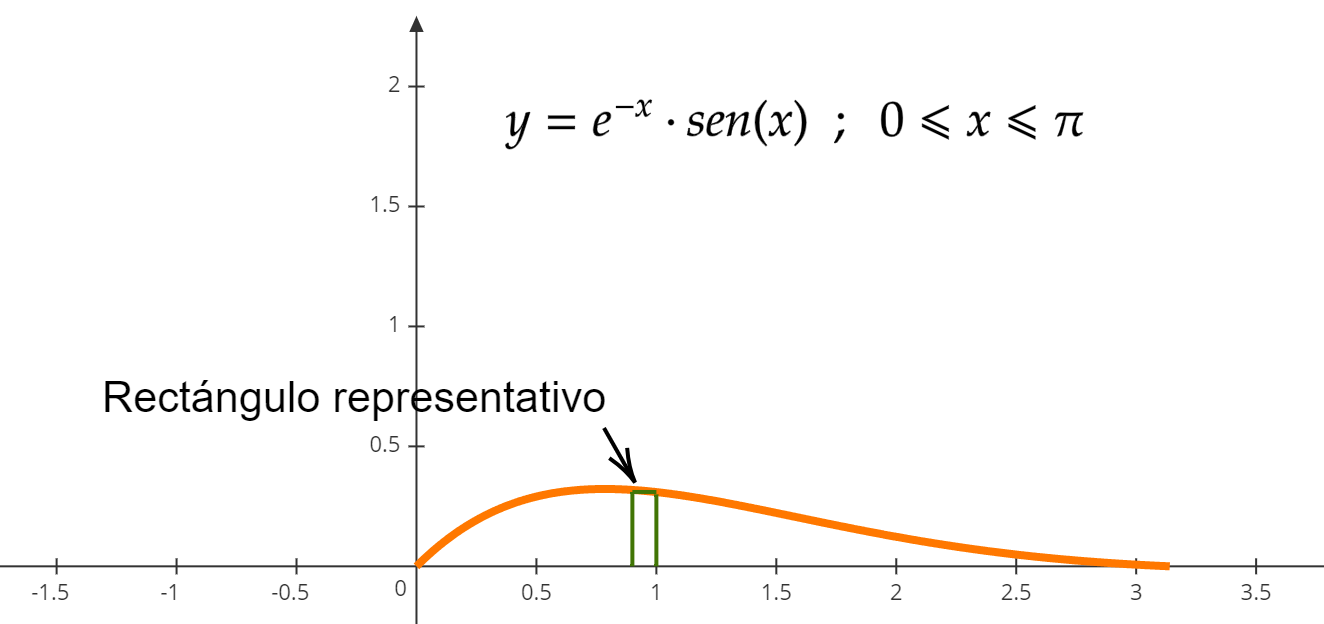
Dibujamos un rectángulo representativo y le hallamos su área, es decir:

\(dA=f( x) dx\longrightarrow Puesto\ que\ estamos\ calculando\ el\ área\ con\ respecto\ a\ x. \\\) \(dA=\left[ e^{-x} \cdot sen( x)\right] dx\)

Ahora bien, como queremos saber el área de todos los posibles rectángulos que componen esa región de área limitada por el eje \( x \ \ y \ \ el \ \ intervalo \ \  [0,\pi]\)

\(\int dA=\int e^{-x} \cdot sen( x) dx \\\) \(A=\int _{0}^{\pi } e^{-x} \cdot sen( x) dx\)

Resolviendo la integral:

Usamos la técnica de integración por partes:

\(u=\ sen( x) \ \ \ \land \ \ \ dv=\ e^{-x} dx\\\) \(du=cos( x) dx\ \land \ \ \ \ v=-e^{-x} \\\) \(A=\int _{0}^{\pi } e^{-x} \cdot sen( x) dx=-e^{-x} sen( x) -\int _{0}^{\pi }\left( -e^{-x} \cdot cos( x)\right) dx \\\) \(A=\int _{0}^{\pi } e^{-x} \cdot sen( x) dx=-e^{-x} sen( x) +\int _{0}^{\pi } e^{-x} \cdot cos( x) dx\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Eq.\ ( 1) \\\)

Resolviendo \(\int _{0}^{\pi } e^{-x} \cdot cos( x) dx\)

\(u_{1} =cos( x) \ \ \ \ \ \ \ \ \ \land \ \ \ \ dv_{1} =e^{-x} dx \\\) \(du_{1} =-sen( x) dx\ \land \ \ \ \ \ \ v_{1} =-e^{-x} \\\) \(\int _{0}^{\pi } e^{-x} \cdot cos( x) dx=-e^{-x} cos( x) -\int _{0}^{\pi }\left[ -e^{-x}( -sen( x))\right] dx \\\) \(\int _{0}^{\pi } e^{-x} \cdot cos( x) dx=-e^{-x} cos( x) -\int _{0}^{\pi } e^{-x} \cdot sen( x)) dx\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Eq.\ (2)\)

Ahora bien, reemplazamos \(Eq.\ ( 2) \ \  en \ \  Eq.\ (1)\)

\(A=\int _{0}^{\pi } e^{-x} \cdot sen( x) dx=-e^{-x} sen( x) -e^{-x} cos( x) -\int _{0}^{\pi } e^{-x} \cdot sen( x)) dx \\\) \(A=2\int _{0}^{\pi } e^{-x} \cdot sen( x) dx=-e^{-x} sen( x) -e^{-x} cos( x) \\\) \(A=2\int _{0}^{\pi } e^{-x} \cdot sen( x) dx=-e^{-x}( sen( x) +cos( x)) \\\) \(A=\int _{0}^{\pi } e^{-x} \cdot sen( x) dx=-\frac{e^{-x}}{2}( sen( x) +cos( x))\)

Ahora bien, hacemos uso del TEOREMA FUNDAMENTAL DEL CALCULO – Parte 2

\(Sea\ \int _{a}^{b} f( x) dx\ =\ F( x)]_{a}^{b} =F( b) \ -F( a) \\\) \(A=-\frac{e^{-x}}{2}( sen( x) +cos( x)) \\\) \(A=\left[ -\frac{e^{-\pi }}{2}( sen( \pi ) +cos( \pi ))\right] -\left[ -\frac{e^{-0}}{2}( sen( 0) +cos( 0))\right] \\\) \(A=-\frac{e^{-\pi }}{2}( 0-1) +\frac{1}{2}( 0+1) \\\) \(A=\frac{e^{-\pi }}{2} +\frac{1}{2} \\\) \(A=\frac{e^{-\pi } +1}{2} \\\) \(A=0,522\ und^{2}\)

Gracias por llegar hasta acá, espero que te haya gustado tanto como disfruto escribiendo. Nos vemos pronto. Has parte de la comunidad matemática más grande de la Unimagdalena y Santa Marta. Click aquí: https://www.facebook.com/integracadadia/

Recommended1 Me gustaPublicado en Ingeniería, Matemáticas