La técnica de integración por partes es otro de los métodos usados frecuentemente en el cálculo de integrales indefinidas. Junto con la técnica de integración por sustitución o cambio de variable se considera, en algunas partes, los únicos dos métodos de integración, pero hoy en día, en diversas instituciones académicas se consideran más métodos que veremos más adelante.
Esta técnica surge a partir de lo que se conoce en calculo diferencial como la derivada de un producto de funciones. A partir de allí, llegaremos a la fórmula deseada.
Sea f(x){f(x)} y g(x){g(x)} diferenciables, tenemos que:
ddx[f(x)⋅g(x)]=f′(x)⋅g(x)+f(x)⋅g′(x)\frac{d}{dx}[f(x) \cdot g(x)] = f'(x) \cdot g(x) + f(x) \cdot g'(x)
Luego, multiplicamos la igualdad por el diferencial de la variable independiente: dx{dx}
d[f(x)⋅g(x)]=[f′(x)⋅g(x)+f(x)⋅g′(x)]dxd[f(x)⋅g(x)]=f′(x)⋅g(x)dx+f(x)⋅g′(x)dx\begin{array}{l} d[f(x) \cdot g(x)] = [f'(x) \cdot g(x) + f(x) \cdot g'(x)]dx \\ \\ d[f(x) \cdot g(x)] = f'(x) \cdot g(x) dx + f(x) \cdot g'(x) dx \end{array}
Integrando a ambos lados tenemos:
∫d[f(x)⋅g(x)]=∫f′(x)⋅g(x)dx+∫f(x)⋅g′(x)dx\int d[ f( x) \cdot g( x)] =\int f'( x) \cdot g( x) dx+\int f( x) \cdot g'( x) dx
Despejamos ∫f(x)⋅g′(x)dx\int f( x) \cdot g'( x) dx
∫f(x)⋅g′(x)dx=∫d[f(x)⋅g(x)]−∫f′(x)⋅g(x)dx\int f( x) \cdot g'( x) dx=\int d[ f( x) \cdot g( x)] -\int f'( x) \cdot g( x) dx
Siendo la derivada y la integración dos operaciones contrarias, nos queda lo siguiente:
∫f(x)⋅g′(x)dx=f(x)⋅g(x)−∫f′(x)⋅g(x)dx\int f( x) \cdot g'( x) dx=f( x) \cdot g( x) -\int f'( x) \cdot g( x) dx
Ahora bien, si hacemos
u=f(x) ∧ dv=g′(x)du=f′(x) ∧ v=g(x)\begin{array}{l} u=f( x) \ \ \land \ dv=g'( x) \\ du=f'( x) \ \land \ \ \ v=g( x) \end{array}
Nos quedaría la siguiente expresión:
∫u⋅dv=u⋅v−∫v⋅du\int u\cdot dv=u\cdot v-\int v\cdot du, QED
Analizando la formula podemos ver que esta técnica nos será útil cuando tengamos productos de funciones. Pero nace la pregunta, ¿Qué tipo de funciones?
Aquí te mostrare algunos casos que se pueden presentar:
Caso I: ∫P(x)⋅eaxdx ; u=P(x) ∧ dv=eaxdxCaso\ I:\ \int P( x) \cdot e^{ax} dx\ ;\ \ \ u=P( x) \ \ \ \ \ \land \ dv=e^{ax} dx
Caso II: ∫P(x)⋅sen(ax)dx u=P(x) ∧ dv=sen(ax)dx Caso\ II:\ \int P( x) \cdot sen( ax) dx\;\ \ \ u=P( x) \ \ \ \ \ \land \ dv=sen( ax) dx\
Caso III: ∫P(x)⋅cos(ax)dx ; u=P(x) ∧ dv=cos(ax)dxCaso\ III:\ \int P( x) \cdot cos( ax) dx\ ;\ \ \ u=P( x) \ \ \ \ \ \land \ dv=cos( ax) dx
Caso IV: ∫P(x)⋅ln(ax)dx u=ln(ax) ∧ dv=P(x)dxCaso\ IV:\ \int P( x) \cdot ln( ax) dx\;\ \ \ u=ln( ax) \ \ \land \ dv=P( x) dx
Caso V: ∫sen(x)⋅ebxdx u=sen(x) ∧ dv=ebxdxCaso\ V:\ \int sen( x) \cdot e^{bx} dx\;\ \ \ u=sen( x) \ \ \land \ dv=e^{bx} dx
Caso VI: ∫cos(ax)⋅ebxdx u=cos(ax) ∧ dv=ebxdxCaso\ VI:\ \int cos( ax) \cdot e^{bx} dx\;\ \ \ u=cos( ax) \ \land \ dv=e^{bx} dx
Donde a ∧ b son constantes ∈ Ra\ \land \ b\ son\ constantes\ \in \ \mathbb{R}
Pero estos no son todos los posibles casos que se pueden llevar a cabo por medio de la integración por partes. Existe una regla que encierra un gran número de casos, aunque no siempre es exitosa.
ILATE – Regla
Nos sirve para la escogencia adecuada del uu y dvdv. Esta regla agrupa las 55 funciones elementales en 55 clases. Las ordena de forma descendente tomando como criterio la dificultad para hallar su antiderivada, de difícil a fácil.
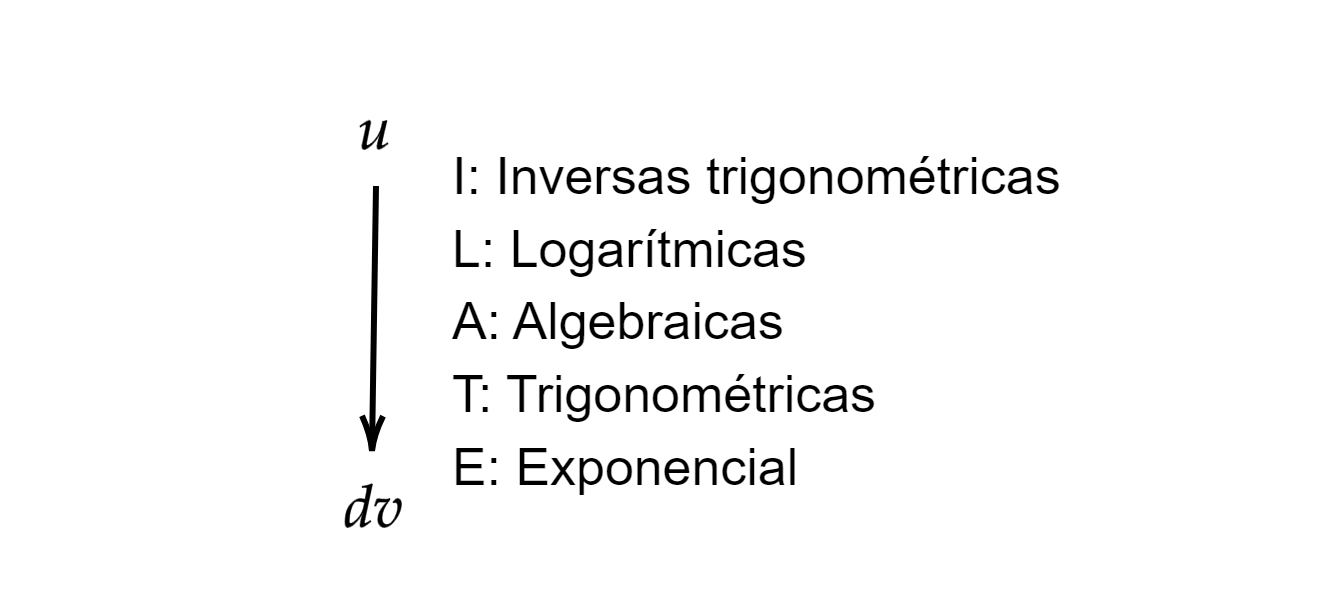
Con esta simple regla ya podemos ampliar los casos que se pueden solucionar usando la técnica de integración por partes.
Por otro lado, en muchas ocasiones vamos a tener que usar la técnica varias veces. Por ejemplo:
Resuelva ∫x3⋅e6xdx\int{}x^{3}⋅e^{6x}dx
Solución
De acuerdo a ILATE,
f(x)=x3,función algebraica g(x)=e6x,función exponencialf(x)=x^{3} , función \ algebraica \ \ g(x)=e^{6x}, función \ \ exponencial
u=x3 ∧ dv=e6xdx du=3x2dx ∧ v=16e6xu= x^{3} \ \ ∧ \ \ dv=e^{6x}dx \ \ du=3x^{2}dx \ \ ∧ \ \ v=\frac{1}{6}e^{6x}
∫x3⋅e6xdx=16x3e6x−36∫x2⋅er6xdx\int{}x^{3}⋅e^{6x}dx=\frac{1}{6}x^{3}e^{6x}-\frac{3}{6}\int{}x^{2}⋅e^r{6x}dx
∫x3⋅e6xdx=16x3e6x−12∫x2⋅e6xdx(1)\int{}x^{3}⋅e^{6x}dx=\frac{1}{6}x^{3}e^{6x}-\frac{1}{2}\int{}x^{2}⋅e^{6x}dx (1)
Resolviendo ∫x2⋅e6xdx\int{}x^{2}⋅e^{6x}dx
\(u_{1}=x^{2} \ \ ∧ \ \ dv_{1}=e^{6x}dx \ \ du_{1}=2xdx \ \ ∧ \ \ dv_{1}=\frac{1}{6}e^{6x} \)u1=x2∧dv1=e6xdxdu1=2xdx∧dv1=16e6x
∫xr2⋅e6xdx=16x2e6x−26∫xe6xdx\int{}x^r{2}⋅e^{6x}dx=\frac{1}{6}x^{2}e^{6x}-\frac{2}{6}\int{}xe^{6x}dx
∫x2⋅e6xdx=16x2e6x−13∫xe6xdx(2)\int{}x^{2}⋅e^{6x}dx=\frac{1}{6}x^{2}e^{6x}-\frac{1}{3}\int{}xe^{6x}dx (2)
Resolviendo ∫xe6xdx\int{}xe^{6x}dx
u2=x∧dv2=e6xdx du2=dx∧v2=16e6xu_{2}=x ∧ dv_{2}=e^{6x}dx \ \ du_{2}=dx ∧ v_{2}=\frac{1}{6}e^{6x}
∫xe6xdx=16xe6x−16∫e6xdx\int{}xe^{6x}dx=\frac{1}{6}xe^{6x}-\frac{1}{6}\int{}e^{6x}dx
∫xe6xdx=16xe6x−136e6x+c1(3)\int{}xe^{6x}dx=\frac{1}{6}xe^{6x}-\frac{1}{36}e^{6x}+c_{1} (3)
Reemplazando (3)(3) en (2)(2)
∫x2⋅e6xdx=16x2e6x−13(16xe6x−136e6x)+c2\int{}x^{2}⋅e^{6x}dx=\frac{1}{6}x^{2}e^{6x}-\frac{1}{3}(\frac{1}{6}xe^{6x}-\frac{1}{36}e^{6x})+c_{2}
∫x2⋅e6xdx=16x2e6x−118xe6x+1108e6x+c2(4)\int{}x^{2}⋅e^{6x}dx=\frac{1}{6}x^{2}e^{6x}-\frac{1}{18}xe^{6x}+\frac{1}{108}e^{6x}+c_{2} (4)
Reemplazando (4)(4) en (1)f(1)
∫x3⋅e6xdx=16x3e6x−12(16x2e6x−118xe6x+1108e6x)+C\int{}x^{3}⋅e^{6x}dx=\frac{1}{6}x^{3}e^{6x}-\frac{1}{2}(\frac{1}{6}x^{2}e^{6x}-\frac{1}{18}xe^{6x}+\frac{1}{108}e^{6x})+C
∫x3⋅e6xdx=16x3e6x−112x2e6x+136xe6x−1216e6x+C\int{}x^{3}⋅e^{6x}dx=\frac{1}{6}x^{3}e^{6x}-\frac{1}{12}x^{2}e^{6x}+\frac{1}{36}xe^{6x}-\frac{1}{216}e^{6x}+C
Podemos sacar factor común 16e6x\frac{1}{6}e^{6x}, ¡Inténtalo!
Pdta: Existen otros artificios para simplificar estos cálculos que en muchas ocasiones resultan ser laboriosos. Por ejemplo, integración tabular o derivar las dos funciones.
Finalmente, también nos encontraremos con integrales indefinidas llamadas cíclicas. El concepto de cíclico es sinónimo de repetido o bucle infinito. Básicamente, una integral cíclica es aquella que cuando estamos resolviéndola vuelve a aparecer en la solución. Por ejemplo:
Resuelva ∫sen(x)⋅exdx\int{}sen(x)⋅e^{x}dx
Solución
u=sen(x)∧dv=exdx du=cos(x)dx∧v=exu=sen(x) ∧ dv=e^{x}dx \ \ du=cos(x)dx ∧ v=e^{x}
∫sen(x)⋅exdx=sen(x)ex−∫cos(x)exdx(1)\int{}sen(x)⋅e^{x}dx=sen(x)e^{x}-\int{}cos(x)e^{x}dx (1)
Resolviendo ∫cos(x)exdx\int{}cos(x)e^{x}dx
u1=cos(x)∧dv1=exdx du1=−sen(x)dx∧v1=exu_{1}=cos(x) ∧ dv_{1}=e^{x}dx \ \ du_{1}=-sen(x)dx ∧ v_{1}=e^{x}
∫cos(x)exdx=cos(x)ex+∫sen(x)exdx(2)\int{}cos(x)e^{x}dx=cos(x)e^{x}+\int{}sen(x)e^{x}dx (2)
Vemos que vuelve a aparecer la integral y esto se repite nn veces.
Miremos, reemplazando (2)(2) en (1)(1)
∫sen(x)⋅exdx=sen(x)ex−(cos(x)ex+∫sen(x)exdx)\int{}sen(x)⋅e^{x}dx=sen(x)e^{x}-(cos(x)e^{x}+\int{}sen(x)e^{x}dx)
∫sen(x)⋅exdx=sen(x)ex−cos(x)ex−∫sen(x)exdx\int{}sen(x)⋅e^{x}dx=sen(x)e^{x}-cos(x)e^{x}-\int{}sen(x)e^{x}dx
Vemos que podemos despejar ∫sen(x)exdx\int{}sen(x)e^{x}dx
∫sen(x)⋅exdx+∫sen(x)exdx=sen(x)ex−cos(x)ex\int{}sen(x)⋅e^{x}dx+\int{}sen(x)e^{x}dx=sen(x)e^{x}-cos(x)e^{x}
2∫sen(x)exdx=sen(x)ex−cos(x)ex+C2\int{}sen(x)e^{x}dx=sen(x)e^{x}-cos(x)e^{x}+C
∫sen(x)exdx=ex[sen(x)−cos(x)]2+C\int{}sen(x)e^{x}dx=\frac{e^{x}[sen(x)-cos(x)]}{2}+C
Recommended4 dieron "Me gusta"Publicado en Ingeniería, Matemáticas



















Comentarios