En muchos escenarios del cálculo de integrales indefinidas nos vamos a encontrar con integrales que
no son inmediatas o bien, integrales que no contienen una forma estándar. Es por eso que debemos buscar alguna solución para hallar estas antiderivadas.
Las técnicas de integración son métodos que nos ayudan a llevar una integral indefinida a integrales ya conocidas, aquí recae la importancia de su estudio. Dentro de estas técnicas de integración está la técnica de integración por sustitución o cambio de variable, la cual vamos a conocer de dónde proviene.
La aparición de esta técnica de integración se fundamenta en la derivada de una función compuesta (Cálculo diferencial), esto es:
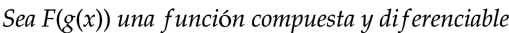
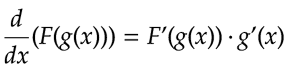
Nos interesa el diferencial, por lo tanto:
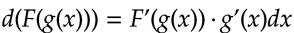
Luego, si integramos a ambos lados de la ecuación nos quedaría:
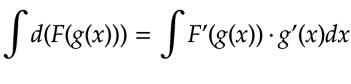
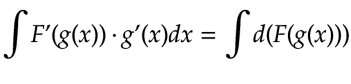
Siendo la derivada y la integración, dos operaciones inversas, tenemos:
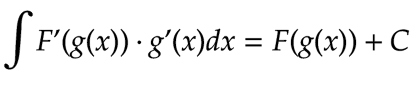
Ahora, vamos a demostrar porque esto es cierto. Realizaremos el siguiente cambio de variable:
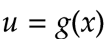
Luego, le hallamos su diferencial:
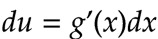
Recuerda: El diferencial de una función viene dado por la derivada de la función multiplicado por el diferencial de la variable independiente.
Podemos reescribir la integral ahora en términos de la nueva variable que definimos:
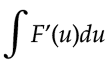
Luego, podemos ver que nos queda una integral mucho mas sencilla de resolver, una integral estándar o inmediata. Si F es un antiderivada, tenemos:
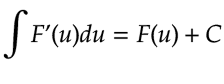
Recuerda: Se debe agregar una constante arbitraria puesto que existen infinitas antiderivadas de una función.
En este paso, debemos volver a nuestra variable original. Usamos el siguiente hecho:
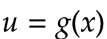
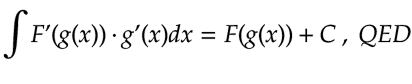
Si queremos demostrar que nuestro procedimiento está bien, podemos derivar la solución y esta debe ser igual a la función integrando.
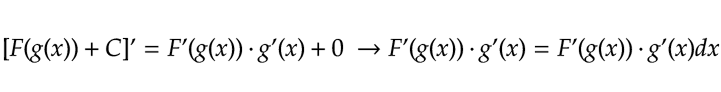
Recuerda: Para derivar una función compuesta necesitamos derivar la función externa y esta la multiplicamos con la derivada de la función interna.
En conclusión, vemos que la derivada de la solución de la integral es igual a la función integrando.
TEOREMA
En virtud de lo anterior, podemos establecer el siguiente teorema: Sustitución de las integrales indefinidas:
Sea g una función derivable y supongamos que F es una antiderivada de f . Entonces si hacemos u=g(x), tenemos:
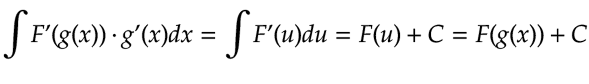
ALGUNAS CONCLUSIONES IMPORTANTES
De aquí, podemos concluir las siguientes propiedades:
Si tenemos
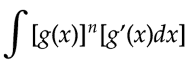
Resulta muy útil expresar la x en función de u para poder realizar con éxito la sustitución. Es decir,
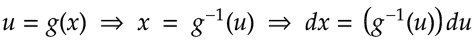
Por lo que, si g es una función diferenciable y n ≠ -1 es un número racional, entonces,
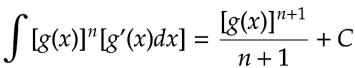
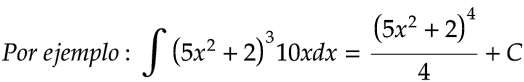
Si tenemos
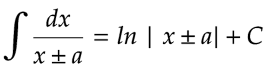
Esto es cierto puesto que:
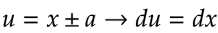
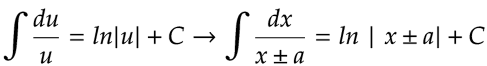
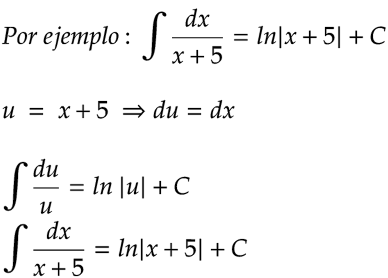
Puedes aprender más aquí: https://www.facebook.com/integracadadia
Recommended2 dieron "Me gusta"Publicado en Biología, Educación, Ingeniería, Ingeniería agronómica, Ingeniería ambiental y sanitaria, Ingeniería civil, Ingeniería de sistemas, Ingeniería electrónica, Ingeniería industrial, Ingeniería pesquera, Matemáticas, Programación





















Comentarios