Ingeniería, Matemáticas

Integrales impropias. Todo lo que debes de saber

FABIAN EDUARDO CASTILLO GONZALEZ

Visitas totales: 547

Las integrales impropias son un tipo de integrales en el que uno o ambos límites de integración tienden al infinito, o en las que el integrando tiene una asíntota dentro del intervalo de integración.

Integrales impropias tipo I: Integrales con límites de integración infinitos

i) $Si \ \ f \ \ es \ \ continua \ \ en \ \ ( \infty ,a] ,\ \ entonces \\ \int _{-\infty }^{a} f(x) dx=\lim _{t\rightarrow -\infty }\int _{t}^{a} f(x) dx,\ \ si \ \ el \ \ límite \ \ existe$

ii) $Si \ \ f \ \ es \ \ continua \ \ en \ \ ( \infty ,a] ,\ \ entonces \\ \int _{-\infty }^{a} f( x) dx=\lim _{t\rightarrow -\infty }\int _{t}^{a} f( x) dx, \ \ si \ \ el\ \ límite\ \ existe.$

iii)$Si\ f\ es\ continua\ en\ el\ intervalo\ ( -\infty ,\infty ) , entonces\\ \int _{-\infty }^{\infty } f( x) dx=\int _{-\infty }^{a} f( x) dx+\int _{a}^{\infty } f( x) dx =\lim _{t\rightarrow -\infty }\int _{t}^{a} f( x) dx+\lim _{t\rightarrow \infty }\int _{a}^{t} f( x) dx, \\ si \ \ ambos \ \ límites \ \ existen, \ \ donde \ \ a \int ( -\infty ,\infty ) .$

Si en cada caso los límites que intervienen existen, diremos que la integral impropia converge y el valor de la integral es el valor del límite calculado o la suma de los límites, de modo contrario, diremos que la integral es divergente.

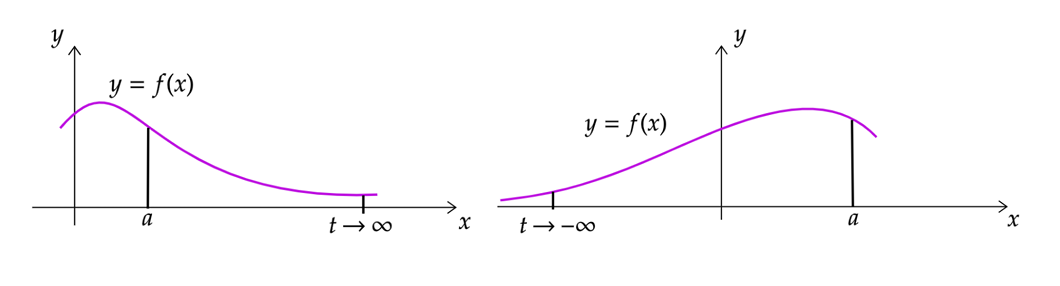
Integrales impropias tipo II: Integrando discontinuos

i)$ Si \ \ f \ \ es \ \ continua \ \ en \ \ [ a,b) \ \ y \ \ discontinua \ \ en \ \ b \ \ ( tiene \ \ una \ \ asíntota \ \ vertical \ \ en \ \ x \ \ =b) ,\ \\ entonces \ \ \int _{a}^{b} f( x) dx=\lim _{t\rightarrow b^{-}}\int _{a}^{t} f( x) dx,\ si \ \ el \ \ límite \ \ existe. $

ii)$Si \ \ f \ \ es \ \ continua \ \ en \ \ ( a,b] \ \ y \ \ discontinua \ \ en \ \ a \ \ ( tiene \ \ una \ \ asíntota \ \ vertical \ \ en \ \ x=a) ,\\ entonces\ \int _{a}^{b} f( x) dx=\lim _{t\rightarrow a^{+}}\int _{t}^{b} f( x) dx, \ \ si \ \ el \ \ límite \ \ existe. $

iii)$Si \\ la \ \ función \ \ f \ \ es \ \ continua \ \ en \ \ el \ \ intervalo \ \ [ a,b] \ \ con \ \ excepción \ \ de \ \ x \ \ = \ \ c \ \ \in \ ( a,b) ,\\ \ y \ \ si \ \ en \ \ x=c \ \ la \ \ gráfica \ \ de \ \ f \ \ tiene \ \ una \ \ asíntota \ \ vertical \ \ entonces \ \ \\ \int _{a}^{b} f( x) dx=\int _{a}^{c} f( x) dx+\int _{c}^{b} f( x) dx=\lim _{t\rightarrow c^{-}}\int _{a}^{t} f( x) dx+\lim _{t\rightarrow c^{+}}\int _{t}^{b} f( x) dx $

Una vez más, si en cada caso los límites que intervienen existen, diremos que la integral impropia converge y el valor de la integral es el valor del límite calculado o la suma de los límites, de modo contrario, diremos que la integral es divergente.

Ejemplo

Resuelve $\int _{-\infty }^{\infty }\frac{dx}{x^{2} +2x+2}$

Solución

Esta integral corresponde a las integrales impropias tipo I: Integrales con límites de integración infinitos.

iii) $ Si \ \ f \ \ es \ \ una \ \ función \ \ continua \ \ en \ \ el \ \ intervalo \ \ R \ \ =\ ( -\infty ,\infty ) ,\\ entonces:\\ \int _{-\infty }^{\infty } f( x) dx=\int _{-\infty }^{a} f( x) dx+\int _{a}^{\infty } f( x) dx=\lim _{t\rightarrow -\infty }\int _{t}^{a} f( x) dx+\lim _{t\rightarrow \infty }\int _{a}^{t} f( x) dx \\ Si \ \ ambos \ \ límites \ \ existen, \ \ donde \ \ a \ \ es \ \ cualquier \ \ constante \ \ en \ \ R.$

En virtud de esto y siendo $a=0, \ \ \in \ \ R$, tenemos que:

$\int _{-\infty }^{0}\frac{dx}{x^{2} +2x+2} +\int _{0}^{\infty }\frac{dx}{x^{2} +2x+2} =\lim _{t\rightarrow -\infty }\int _{t}^{0}\frac{dx}{x^{2} +2x+2} +\lim _{t\rightarrow \infty }\int _{0}^{t}\frac{dx}{x^{2} +2x+2}$

Resolviendo $\int \frac{dx}{x^{2} +2x+2}$$

Completación de cuadrados:

$x^{2} +2x+2=0\rightarrow x^{2} +2x=-2\rightarrow \left( x^{2} +2x+1\right) =-2+1\\ ( x+1)^{2} =-1\rightarrow ( x+1)^{2} +1=0$

¡Recuerda!

$Producto \ \ notable:\ ( a\pm b)^{2} =a^{2} \pm 2ab+b^{2}$
$\int \frac{dx}{( x+1)^{2} +1}$

Sustitución simple:

$u=x+1\rightarrow du=dx$ $\int \frac{du}{u^{2} +1} =tan^{-1}( u) +C$

Volviendo a la variable original, tenemos:

$\int \frac{dx}{( x+1)^{2} +1} =tan^{-1}( x+1) +C$

Ahora bien,

$\int _{-\infty }^{\infty }\frac{dx}{x^{2} +2x+2} =\lim _{t\rightarrow -\infty }\left[ tan^{-1}( x+1)\right]_{t}^{0} +\lim _{t\rightarrow \infty }\left[ tan^{-1}( x+1)\right]_{t}^{0}$

¡Recuerda!

$Teorema \ \ Fundamental \ \ del \ \ Cálculo \ \ – \ \ Parte \ \ 2\\ \int _{a}^{b} f( x) dx=F( x)]_{a}^{b} =F( b) -F( a)$
$\lim _{t\rightarrow -\infty }\left[ tan^{-1}( 0+1) -tan^{-1}( t+1)\right] +\lim _{t\rightarrow \infty }\left[ tan^{-1}( 0+1) -tan^{-1}( t+1)\right]$
$\lim _{t\rightarrow -\infty }\left[ tan^{-1}( 1) -tan^{-1}( t+1)\right] +\lim _{t\rightarrow \infty }\left[ tan^{-1}( 1) -tan^{-1}( t+1)\right]$
$\int _{-\infty }^{\infty }\frac{dx}{x^{2} +2x+2} =-\left( -\frac{\pi }{2}\right) +\frac{\pi }{2} =\frac{\pi }{2} +\frac{\pi }{2} =\frac{2\pi }{2}$

$\int _{-\infty }^{\infty }\frac{dx}{x^{2} +2x+2} =\pi$

Los límites involucrados existen, por lo tanto, la integral impropia converge y el valor de la integral es $\pi$

Ahora es tú turno. Aquí hay un ejercicio resuelto parcialmente:

Calcule el valor de la integral $\int _{1}^{\infty }( 1-x) e^{-x} dx$

Solución

Esta integral corresponde a las integrales impropias tipo I: Integrales con límites de integración infinitos.

$Si \ \ f \ \ es \ \ una \ \ función \ \ continua \ \ en \ \ [ a,\infty ) ,\ \ entonces:\\ \int _{a}^{\infty } f( x) dx=\lim _{t\rightarrow \infty }\int _{a}^{t} f( x) dx, \ \ si \ \ el \ \ límite \ \ existe.\\ \\ Donde \ \ a \ \ es \ \ cualquier \ \ constante \ \ en \ \ [ a,\infty )$

Gracias por llegar hasta acá, espero que te haya gustado tanto como disfruto escribiendo. Nos vemos pronto. Has parte de la comunidad matemática más grande de la Unimagdalena y Santa Marta. Click aquí: https://www.facebook.com/integracadadia/